Teorema de pitágoras
O teorema de Pitágoras é umarelação matemática entre os três lados de qualquer triângulo retângulo. Na geometria euclidiana, o teorema afirma que:
| “ | Em qualquer triângulo retângulo, o quadradodo comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos. | ” |
Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetossão os dois lados que o formam.
O enunciado anterior relaciona comprimentos, mas o teorema também pode ser enunciado como uma relação entre áreas:
| “ | Em qualquer triângulo retângulo, a área doquadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos. | ” |
Para ambos os enunciados, pode-seequacionar:
onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
O teorema de Pitágoras leva o nome do matemático grego Pitágoras (570 a.C. – 495 a.C.), que tradicionalmente é creditado pela sua descoberta e demonstração,[1][2] embora seja frequentemente argumentado que o conhecimento do teorema seja anterior a ele (há muitas evidências de quematemáticos babilônicos conheciamalgoritmos para calcular os lados em casos específicos, mas não se sabe se conheciam um algoritmo tão geral quanto o teorema de Pitágoras).[3] [4] [5]
O teorema de Pitágoras é um caso particular da lei dos cossenos, domatemático persa Ghiyath al-Kashi(1380 – 1429), que permite o cálculo do comprimento do terceiro lado de qualquer triângulo, dados os comprimentos de dois lados e a medida de algum dos três ângulos.
Fórmula e corolários
Sendo c o comprimento da hipotenusa e a e b os comprimentos dos outros dois lados, o teorema pode ser expresso como a equação:
Manipulando algebricamente essa equação, chega-se a que se os comprimentos de quaisquer dois lados do triângulo retângulo são conhecidos, o comprimento do terceiro lado pode ser encontrado:
 ,
,  e
e 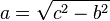 .
.
Outro corolário do teorema é que:
| “ | Em qualquer triângulo retângulo, a hipotenusa é maior que qualquer um dos catetos, mas menor que a soma deles. [6] | ” |
maior que qualquer um dos catetos pois todos os comprimentos são necessariamente números positivos, e c² > b², logo c > b, e c² > a², logo c > a. E a hipotenusa é menor que a soma dos catetos pois c² = b² + a², e (b+a)² = b² + 2ba + a², logo c² < (b+a)², logo c < b + a.
Demonstrações
O teorema de Pitágoras já teve muitas demonstrações publicadas. O livro The Pythagorean Proposition, de Elisha Scott Loomis, por exemplo, contém 370 demonstrações diferentes.[7] Há uma demonstração no livro Os Elementos, de Euclides.[8] E também ofereceram demonstrações, o matemático indiano Bhaskara Akaria, o polímata italianoLeonardo da Vinci, e o vigésimopresidente dos Estados Unidos,James A. Garfield.[9][10][11] O teorema de Pitágoras é tanto uma afirmação a respeito de áreas quanto a respeito de comprimentos, algumas provas do teorema são baseadas em uma dessas interpretações, e outras provas são baseadas na outra interpretação.
Por comparação de áreas
Não se sabe ao certo qual seria a demonstração utilizada porPitágoras, entretanto, muitos autores concordam que ela teria sido feita através da comparação de áreas[carece de fontes], conforme se segue:
- Desenha-se um quadrado de lado b + a;
- Traçam-se dois segmentosparalelos aos lados doquadrado;
- Divide-se cada um destes doisretângulos em dois triângulos retos, traçando as diagonais. Chama-se c o comprimento de cada diagonal;
- A área da região formada ao retirar os quatro triângulos retos é igual a b2 + a2;
- Desenha-se agora o mesmo quadrado de lado b + a, mas colocamos os quatro triângulos retos noutra posição.
- A área da região formada quando se retiram os quatro triângulos retos é igual a c2.
Como b2 + a2 representa a área do quadrado maior subtraída da soma das áreas dos triângulos retângulos, e c2 representa a mesma área, então b2 + a2 = c2. Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. O segmento de medida c foi chamado de hipotenusa e os de medida b e a foram chamados de catetos.
Por semelhança de triângulos

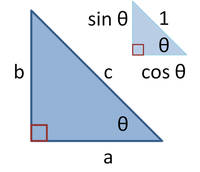
Demonstração que utiliza o conceito de semelhança: os triângulos ABC, ACH e CBH têm a mesma forma, diferindo apenas pelas suas posições e tamanhos.
Esta demonstração se baseia naproporcionalidade dos lados de dois triângulos semelhantes, isto é, que arazão entre quaisquer dois lados correspondentes de triângulos semelhantes é a mesma, independentemente do tamanho dos triângulos.
Sendo ABC um triângulo retângulo, com o ângulo reto localizado em C, como mostrado na figura. Desenha-se a altura com origem no ponto C, e chama-se H sua intersecção com o lado AB. O ponto H divide o comprimento da hipotenusa, c, nas partes d e e. O novo triângulo, ACH, é semelhante ao triângulo ABC, pois ambos tem um ângulo reto, e eles compartilham o ângulo em A, significando que o terceiro ângulo é o mesmo em ambos os triângulos também,[12] marcado como θ na figura. Seguindo-se um raciocínio parecido, percebe-se que o triângulo CBH também é semelhante à ABC. A semelhança dos triângulos leva à igualdade das razões dos lados correspondentes:
Estas relações podem ser escritas como:
Somando estas duas igualdades, obtém-se
que, rearranjada, é o teorema de Pitágoras:
Demonstração algébrica
A análise da figura da direita permite computar a área do quadrado construído sobre a hipotenusa de um triângulo retângulo: ela é quatro vezes a área desse triângulo mais a área do quadrado restante, de lado (b−a). Equacionando-se, segue que:

- Segue que:
 (o termo (b-a)² é um produto notável)
(o termo (b-a)² é um produto notável) (porcomutatividade damultiplicação: 2ab = 2ba)
(porcomutatividade damultiplicação: 2ab = 2ba)
Por cálculo diferencial
Pode-se chegar ao teorema de Pitágoras pelo estudo de como mudanças em um lado produzem mudanças na hipotenusa e usando um pouco de cálculo. É uma demonstração baseada na interpretação métrica do teorema, visto que usa comprimentos, não áreas.
Como resultado da mudança da no lado a,
por semelhança de triângulos e para mudanças diferenciais. Então,
que resulta da adição de um segundo termo para as mudanças no lado b.
Pela integração, segue:
Quando a = 0 então c = b, então a "constante" é b2. Logo,
Pelo rearranjo das partes
Uma demonstração por rearranjo é dada pela animação à esquerda. Como a área total e as áreas dos triângulos são constantes, a área preta total é constante também. E a área preta pode ser dividida em quadrados delineados pelos lados a, b, c do triângulo, demonstrando quea2 + b2 = c2.
Na animação à direita, um grande quadrado inicial é formado da área c 2 tornando adjacentes quatro triângulos retângulos idênticos, deixando um pequeno quadrado no centro do grande quadrado, de modo a acomodar a diferença de comprimentos dos lados dos triângulos. Dois retângulos são formados, de lados a e b, movendo-se os triângulos. Incorporando o pequeno quadrado central com um destes retângulos, os dois retângulos são feitos em dois quadrados de áreas a 2 e b 2, mostrando que c 2 = a 2 + b 2.
Recíproca
- "Para qualquer triângulo com lados l, m, e r, se l² + m² = r², então o ângulo entre l e m mede 90°".
ou, usando apenas palavras,
| “ | Se num triângulo o quadrado em um dos lados for igual à soma dos quadrados construídos sobre os dois lados restantes do triângulo, o ângulo formado pelos dois lados restantes do triângulo é um ângulo reto. | ” |
Ela pode ser provada usando-se a lei dos cossenos.
Consequências e usos
Talvez nenhuma outra relaçãogeométrica seja tão utilizada emmatemática como o teorema de Pitágoras. Ao longo dos séculos foram sendo registrados muitos problemas curiosos, cujas resoluções têm como base este famoso teorema [carece de fontes]. É possível utilizar o teorema de Pitágoras em todos os polígonos, pois eles podem ser divididos emtriângulos e esses em triângulos retângulos. E por extensão, a todos os poliedros.
[editar] A diagonal do quadrado
A diagonal do quadrado divide-o em dois triângulos retânguloscongruentes. Sendo 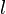 o lado e
o lado e  a diagonal, segue que:
a diagonal, segue que:
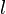 o lado e
o lado e  a diagonal, segue que:
a diagonal, segue que:
Finalmente, o comprimento da diagonal é encontrado como:
A altura do triângulo equilátero
A altura do triângulo equiláterodivide-o em dois triângulos retângulos congruentes. Sendo 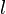 o lado e
o lado e  a altura, segue que:
a altura, segue que:
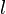 o lado e
o lado e  a altura, segue que:
a altura, segue que:
Finalmente, a altura do triângulo equilátero é encontrado como:
Identidade trigonométrica fundamental
Disso, segue que:
Ternos pitagóricos
Um terno pitagórico (trio pitagórico) consiste em três números inteiros positivos a, b, e c, tais que a 2 + b 2 = c 2. Em outras palavras, um terno pitagórico representa os comprimentos dos lados de um triângulo retângulo, onde todos os três lados têm comprimentos inteiros. Essa tripla é geralmente escrita como (a, b, c ).Alguns exemplos bem conhecidos são (3, 4, 5) e (5, 12, 13).
Um terno pitagórico primitivo é aquele em que a, b e c são coprimos(o máximo divisor comum de a, b e c é 1).
Lista de ternos pitagóricos primitivos até 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Uma das consequências do teorema de Pitágoras é que comprimentosincomensuráveis (ou seja, cujarazão é um número irracional, tal como a raiz quadrada de 2), podem ser construídos, com instrumentos como régua e compasso. Um triângulo retângulo com ambos os catetos iguais a uma unidade tem uma hipotenusa de comprimentoigual a raiz quadrada de 2. A figura da direita mostra como construir segmentos de reta com comprimentos iguais a raiz quadrada de qualquer número inteiro positivo.
Distância entre dois pontos
Seja A = (x1,y1) e B = (x2,y2). Para auxiliar, seja C = (x2,y1).
Como A e C possuem mesmaordenada,  .
.
 .
.
Como B e C possuem mesma abcissa,

Então ![d(A,B)=\sqrt[]{d(A,C)^2+d(B,C)^2}=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}](https://upload.wikimedia.org/math/4/9/3/4937d4e11e24c806976126f07aa7124a.png)
![d(A,B)=\sqrt[]{d(A,C)^2+d(B,C)^2}=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}](https://upload.wikimedia.org/math/4/9/3/4937d4e11e24c806976126f07aa7124a.png)
Generalizações
Lei dos cossenos
O teorema de Pitágoras permite calcular um lado de um triângulo retângulo conhecendo os outros dois. A lei dos cossenos permite calculá-lo em qualquer triângulo. Assim, o teorema de Pitágoras é um caso especial do teorema mais geral que relaciona o comprimento dos lados de qualquer triângulo, a lei dos cossenos é a seguinte:
-
- onde θ é o ângulo entre os lados a e b.
Quando θ é 90 graus, cos(θ) = 0, assim, a fórmula reduz-se ao teorema de Pitágoras.
Teorema de Gua
O teorema de Pitágoras pode ser generalizado para um n-simplex retângulo: o quadrado do (n-1)-volume da hipotenusa é igual à soma dos quadrados dos (n-1)-volumes dos catetos. Em particular, num tetraedro retângulo (isto é, que tem 3 faces perpendiculares entre si - os catetos), o quadrado da área da hipotenusa (a face que não é perpendicular às restantes) é igual à soma dos quadrados das áreas dos catetos.
Figuras semelhantes nos três lados
O teorema de Pitágoras foi generalizado por Euclides em seu livro Os Elementos para estender-se além das áreas dos quadrados nos três lados, para figuras semelhantes:[15]
| “ | Erguendo-se figuras semelhantes nos lados de um triângulo retângulo, então a soma das áreas das duas menores é igual à área da maior. | ” |
Na geometria esférica e hiperbólica
O teorema de Pitágoras é derivado dos axiomas da geometria euclidiana, e de fato, a versão euclidiana não é válida nasgeometrias não euclidianas. (Foi mostrado que o teorema de Pitágoras é equivalente aopostulado das paralelas) Em outras palavras, numa geometria não euclidiana, a relação entre os lados de um triângulo deve necessariamente tomar outra forma. Por exemplo, na geometria esférica, a² + b² ≠ c².
Seja c a hipotenusa de um triângulo rectângulo numa geometria não euclidiana e a e b os catetos. O teorema de Pitágoras toma uma das seguintes formas:
- na geometria esférica, tem-se

- na geometria hiperbólicatem-se



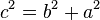

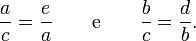

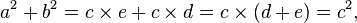




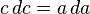









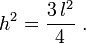


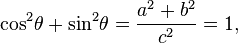




Nenhum comentário:
Postar um comentário